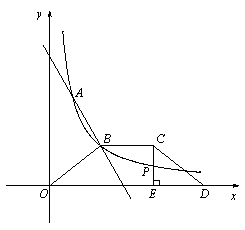
如图,直线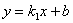 与反比例函数
与反比例函数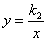 的图象交于A
的图象交于A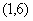 ,B
,B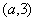 两点.
两点.
(1)求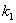 、
、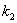 的值;
的值;
(2)直接写出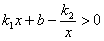 时x的取值范围;
时x的取值范围;
(3)如图,等腰梯形OBCD中,BC//OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
答案
(1)由题意知k2=1×6=6∴反比例函数的解析式为![]() 又B(a,3)在
又B(a,3)在![]() 的图象上,∴a=2,∴B(2,3)∵直线y=k1x+b过A(1,6),B(2,3)两点∴k1+b=62k1+b=3∴解之得:k1=-3,b=9(2)在第一象限∵A点横坐标为1,B点横坐标为2,则x的取值范围为1<x<2在第三象限直线恒在双曲线上方,则x的取值范围为x<0所以x的取值范围是:x<0或1<x<2;(3)当S梯形OBCD=12时,PC=PE.设点P的坐标为(m,n)∵BC∥OD,CE⊥OD,BO=CD,B(2,3)∴C(m,3),CE=3,BC=m-2,OD=m+2∴S梯形OBCD=(BC+OD)×CE×
的图象上,∴a=2,∴B(2,3)∵直线y=k1x+b过A(1,6),B(2,3)两点∴k1+b=62k1+b=3∴解之得:k1=-3,b=9(2)在第一象限∵A点横坐标为1,B点横坐标为2,则x的取值范围为1<x<2在第三象限直线恒在双曲线上方,则x的取值范围为x<0所以x的取值范围是:x<0或1<x<2;(3)当S梯形OBCD=12时,PC=PE.设点P的坐标为(m,n)∵BC∥OD,CE⊥OD,BO=CD,B(2,3)∴C(m,3),CE=3,BC=m-2,OD=m+2∴S梯形OBCD=(BC+OD)×CE×![]() ,即12=(m-2+m+2)×3×
,即12=(m-2+m+2)×3×![]() ∴m=4,又mn=6∴n=
∴m=4,又mn=6∴n=![]() ,即PE=
,即PE=![]() CE∴PC=PE.
CE∴PC=PE.
知识点:一次函数的性质 反比例函数的性质 反比例函数与一次函数的交点问题
(1)先把点A代入反比例函数求得反比例函数的解析式,再把点B代入反比例函数解析式求得a的值,再把点A,B代入一次函数解析式利用待定系数法求得k1的值.(2)直线在双曲线上方,即x的范围是在A,B之间和第三象限,故可直接写出范围.(3)设点P的坐标为(m,n),易得C(m,3),CE=3,BC=m-2,OD=m+2,利用梯形的面积是12列方程,可求得m的值,从而求得点P的坐标,根据线段的长度关系可知PC=PE.
略








