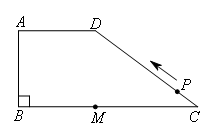
如图，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=6，BC=14，M是BC边上一点，且
MC=8．动点P从点C出发，沿C→D→A→B的路线运动到点B停止．在点P运动的过程中，使△PMC为等腰三角形的点P有(    )

点击查看解析视频：http://v.xxt.cn/course/video.do?id=12619
1．解题要点
①理解题意，整合信息．
对直角梯形进行研究，各线段长如图所示，

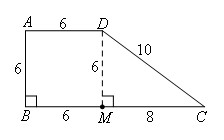
②抓不变特征有序思考，设计方案．
分析定点、动点：△PMC中，C，M是定点，P是动点；
确定分类标准：以CM作等腰三角形的腰或底边来进行分类．
③根据方案作出图形，有序操作．
当CM为腰时，根据等腰三角形两腰相等，分别以点C，M为圆心，CM长为半径作圆，两圆与折线段CD—DA—AB的交点满足题意，进而判断交点个数；
当CM为底边时，点P在线段CM的垂直平分线上，线段CM的垂直平分线与折线段CD—DA—AB的交点满足题意，进而判断交点个数．
④结果检验，总结．
作图验证，根据图形对结果进行判断；分析数据，对结果进行验证取舍．
2．解题过程
以点M为圆心，CM长为半径作圆，交折线段CD—DA—AB于点，
以点C为圆心，CM长为半径作圆，交折线段CD—DA—AB于点，
作线段CM的垂直平分线，交折线段CD—DA—AB于点，
如图所示，

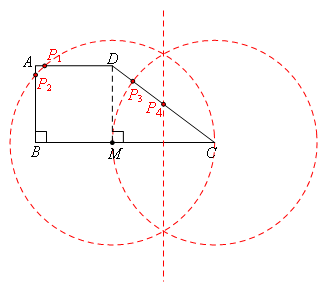
符合题意的点P共有4个．
其中点没有争议，有同学会对以点M为圆心，CM长为半径所作的⊙M与折线段的交点个数有疑问，下面通过计算的方式来说明．
∵⊙M的半径r=8，点M到直线AD的距离d=6，
∴，
∴⊙M与直线AD有两个交点．
如图，设在点D左侧的交点为，连接．

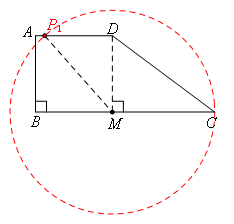
根据勾股定理可求得，
∵，
∴点在线段AD上，
同理可证⊙M与直线AB的一个交点在线段AB上．

略