(上接第2,3题)(3)在(2)的条件下,若抛物线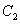 上存在点P(异于点A),使得点P关于直线AF的对称点在x轴上,则点P的坐标为( )
上存在点P(异于点A),使得点P关于直线AF的对称点在x轴上,则点P的坐标为( )
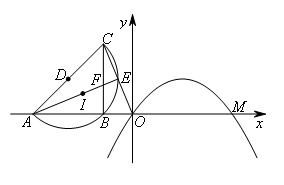
- A.
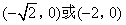
- B.
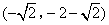
- C.
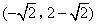
- D.
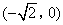
答案
正确答案:C
知识点:二次函数与几何综合
1.解题要点
要找到抛物线![]() 上一点P,使得其关于直线AF的对称点在x轴上,
上一点P,使得其关于直线AF的对称点在x轴上,
其实可以看作是在x轴上存在一点![]() ,其关于直线AF的对称点P在抛物线
,其关于直线AF的对称点P在抛物线![]() 上,
上,
由于点A不仅在抛物线![]() 上,也在x轴上,
上,也在x轴上,
所以直线AP与x轴应该关于直线AF对称,
根据图形可知,直线AP与直线AC重合,
所以直线AC与抛物线的交点即为点P.
2.解题过程
由题意得,直线AC与x轴关于直线AF对称,
所以直线AC与抛物线的交点P满足题意,如图所示,
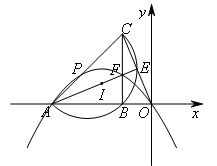
∵AB=BC,∠ABC=90°,![]() ,
,
∴![]() ,
,
联立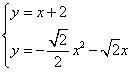 ,解得
,解得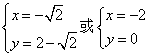 ,
,
∴![]() .
.
略








