如图，在梯形ABCD中，AB∥CD，M为BC的中点，DM平分∠ADC，则下列结论不一定正确的是(    )

如图，延长DM交AB的延长线于点E．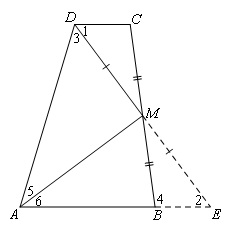

在梯形ABCD中，AB∥CD，
∴∠1=∠2，∠C=∠4．
∵DM平分∠ADC，
∴∠1=∠3，
∴∠2=∠3，
∴AD=AE，即△ADE是等腰三角形．
∵M是BC的中点，
∴CM=BM，
∴△CDM≌△BEM（AAS），
∴DM=EM，CD=BE．
由等腰三角形三线合一得，
∠5=∠6，A对．
DM⊥AM，B对．
∵AE=BE+AB，
∴AD=CD+AB，D对．
对于C，不一定正确，故选C．

略