如图,在矩形ABCD中,DM⊥射线AN于点M,CN⊥AN于点N,G,H分别为MN,CD的中点.若DM=a,GH=b,则CN的长为(用含a,b的代数式表示)( )
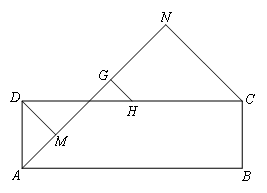
- A.2a+b
- B.a+2b
- C.a+b
- D.2a+2b
答案
正确答案:B
知识点:矩形的性质
思考方向:平行+中点,可考虑类倍长中线.
如图,连接DG并延长,交CN于点J.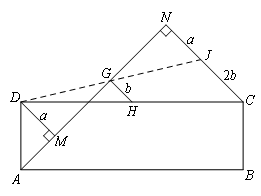
由DM∥CN,G为MN中点,可证△DGM≌△JGN(AAS),
则DM=JN,DG=JG.
又H为CD的中点,
∴GH为△DCJ的中位线,
则GH∥CJ,且![]() .
.
∵DM=a,GH=b,
∴JN=a,CJ=2b,
∴CN=a+2b.
故选B.
略








