如图,在矩形纸片ABCD中,AB=5,AD=3,将纸片折叠,使点B落在边CD上的点B′处,折痕为AE.若在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为( )
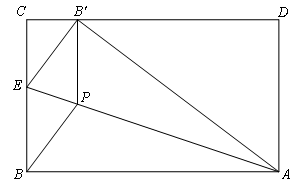
- A.
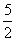
- B.

- C.
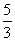
- D.2
答案
正确答案:C
思考方向:由折叠结构,可将P到点B的距离转移到P到点B′的距离,再研究P到CD的距离,根据已知条件,可得PB′⊥CD.延长B′P,可构造矩形.
如图,由折叠性质得,PB=PB′,AB=AB′.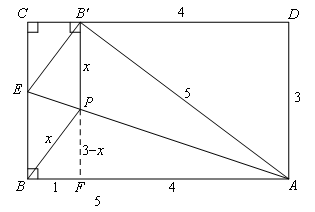
在Rt△AB′D中,由勾股定理可得,B′D=4.
由题意得,PB′的长等于P到CD的距离,则PB′⊥CD.
延长B′P交AB于点F,可证得四边形BFB′C,四边形ADB′F均为矩形,
则AD=FB′,B′D=FA,∠PFB=90°.
设PB=x,则PF=3-x,BF=1.
在Rt△PBF中,由勾股定理,可解得x=![]() ,
,
即所求相等距离为![]() ,故选C.
,故选C.
略








