若E，F，G，H分别为四边形ABCD四条边上的中点，则下列结论错误的是(    )

思考方向：多个中点，考虑组合，利用中位线来处理．
此题无图，需要先画草图，再依图分析．
A：如图，

EF是△ABC的中位线，则EF∥AC，，
同理，HG是△ADC的中位线，则HG∥AC，，
GF是△BCD的中位线，则．
综上，EF∥HG，EF=HG，则四边形EFGH是平行四边形，
又AC=BD，则HG=GF，则四边形EFGH是菱形，故A对．
B：如图，

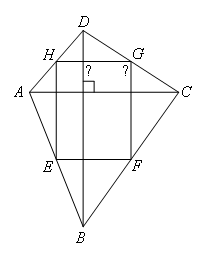
EF是△ABC的中位线，则EF∥AC，，
同理，HG是△ADC的中位线，则HG∥AC，，
GF是△BCD的中位线，则FG∥BD．
综上，EF∥HG，EF=HG，则四边形EFGH是平行四边形，
又AC⊥BD，可证∠HGF=90°，则四边形EFGH是矩形，故B错．
C：如图，

HG是△ADC的中位线，则HG∥AC，
同理，GF是△BCD的中位线，则FG∥BD，
若四边形EFGH是矩形，则∠HGF=90°，
通过平行可导角，进而可证明AC⊥BD，故C对．
D：如图，

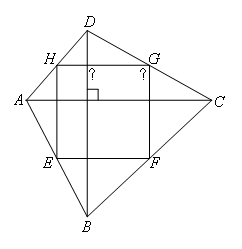
EF是△ABC的中位线，则EF∥AC，，
同理，HG是△ADC的中位线，则HG∥AC，，
GF是△BCD的中位线，则．
综上，EF∥HG，EF=HG，则四边形EFGH是平行四边形，
又AC=BD，则HG=GF，则四边形EFGH是菱形，
又BD⊥AC，通过平行导角，可证明∠HGF=90°，
则四边形EFGH是正方形，故D对．
故选B．

略