如图，在等腰梯形ABCD中，AD∥BC，AB=DC=50，AD=75，BC=135．点P从点B出发，沿折线段BA-AD-DC以每秒5个单位长度的速度向点C匀速运动；点Q从点C出发，沿线段CB以每秒3个单位长度的速度匀速运动．过点Q向上作射线QK⊥BC，交折线段CD-DA-AB于点E．点P，Q同时开始运动，当点P与点C重合时停止运动，点Q也随之停止．设点P，Q运动的时间为t秒（）．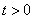
（1）当运动终止时，线段BQ的长为(    )

1．解题要点
无论是动点处理框架，还是图形运动处理框架，操作步骤都是一致的，
①研究基本图形；
②分析运动过程，分段，定范围；
③设计方案求解（动点中是分析几何特征、表达、设计方案求解；图形运动中是分段画图，设计方案表达面积）．
2．解题过程
点P从点B出发，沿折线段BA-AD-DC运动，到点C停止，
点Q从点C出发沿线段CB运动，当点P停止运动时，点Q也停止运动．
根据题意，画出点P，Q运动的线段图，如图所示，

由线段图可知，
当运动终止时，，
点Q运动的路程为，
∴，
故选D．
注意，题目是动点问题的第一问，需要将基本图形研究清楚（如等腰梯形作双高来研究）．
如图，过点A作AM⊥BC于点M，过点D作DN⊥BC于点N．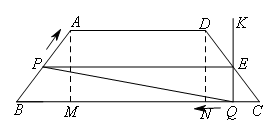

易得MN=AD=75，BM=CN=30，DN=40，
△CND是三边之比为3：4：5的直角三角形，且当运动终止时，QK恰好运动到AM的位置．

略