如图，抛物线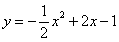与y轴交于点A，顶点为P，△ABC为等腰直角三角形（点B为直角顶点，且AB∥x轴），点C的坐标为（4，3）．平移抛物线，使顶点P在直线AC上滑动，且
与AC交于另一点Q．取BC的中点N，连接NQ，BQ，则的最大值为(    )

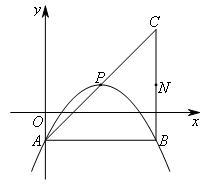
• A.
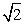
• B.2
• C.
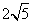
• D.

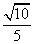
答案

正确答案：D

知识点：二次函数与几何综合  轴对称——线段之和最小  

由题意得，B（4，-1），N（4，1）．
设平移前抛物线的顶点为，则，
∴点在AC上，且．
顶点P在直线AC上滑动的过程中，为定值．
要求的最大值，需先求出NQ+BQ的最小值．
如图，作点B关于直线AC的对称点，

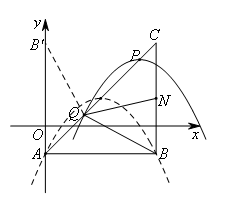
则，，点的坐标为（0，3）．
当三点共线时，的值最小，如图所示，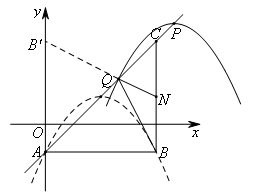

此时．
易求得，
∴的最大值为．

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>