如图,在平面直角坐标系中,已知A(0,4),B(4,0),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.若P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O,D,B三点的抛物线于点E,连接CE.若△BPF与△FCE相似,则点P的坐标为( )
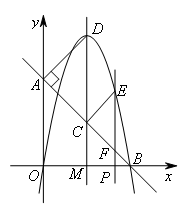
- A.
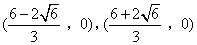
- B.
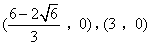
- C.

- D.
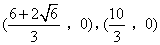
答案
正确答案:D
知识点:相似三角形的存在性
1.解题要点
①首先研究基本图形,△AOB是等腰直角三角形,
其次根据∠DAB=90°,利用三等角模型,求出点D的坐标,
进而能求出抛物线解析式及点C的坐标.
②分析△BPF与△FCE.
△BPF中,B是定点,∠BPF=90°不变,△BPF是等腰直角三角形;
△FCE中,C是定点,∠CFE=45°不变,若△BPF和△FCE相似,
只需满足∠CEF=90°或∠FCE=90°.
③画出符合题意的图形.
当∠CEF=90°时,CE∥BM,先确定点E的坐标,进而确定点P的坐标;
当∠FCE=90°时,CE⊥AB,可先求出直线CE的解析式,确定点E的坐标,
进而确定点P的坐标.
用等腰直角三角形的性质来建等式的几何方法,学生可自行尝试.
2.解题过程
∵A(0,4),B(4,0),
∴△AOB是等腰直角三角形,∠OBA=45°.
如图,过点D作DG⊥y轴于点G.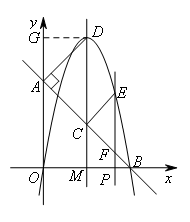
则四边形GOMD为矩形,
∴DG=OM,GO=DM=6.
∵∠DAC=90°,
∴∠GAD=∠GDA=45°,
∴AG=DG.
∵AO=4,
∴AG=DG=2,
∴OM=2,BM=2,
∴C(2,2),D(2,6).
易求抛物线的解析式为![]() .
.
①当∠CEF=90°时,如图所示,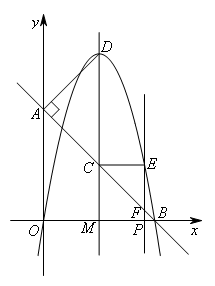
点E和点C的纵坐标都为2,
当![]() 时,解得
时,解得![]() ,
,
由题意得点P(或点E)的横坐标x应满足![]() ,
,
∴![]() ,
,
∴![]() .
.
②当∠FCE=90°时,如图所示,
∵![]() ,
,
∴![]() ,
,
联立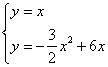 ,解得
,解得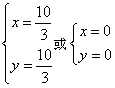 ,
,
∴![]() ,
,
∴![]() .
.
综上,符合题意的点P的坐标为![]() .
.
略








