如图,在平面直角坐标系中,Rt△AOB的两条直角边OA,OB分别在y轴和x轴的正半轴上,并且OA,OB的长分别是方程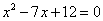 的两根
的两根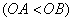 .动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B出发,在线段BA上以每秒2个单位长度的速度向点A运动,设点P,Q运动的时间为t秒.当△APQ与△AOB相似时,t的值为( )
.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B出发,在线段BA上以每秒2个单位长度的速度向点A运动,设点P,Q运动的时间为t秒.当△APQ与△AOB相似时,t的值为( )
- A.
- B.
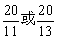
- C.

- D.

答案
正确答案:C
知识点:相似三角形的存在性
1.解题要点
①分析基本图形,OB=4,OA=3,AB=5;
分析运动状态,如图所示,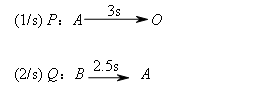
∴![]() .
.
②目标△AOB是三边之比为3:4:5的直角三角形;
△APQ中,A是定点,P,Q是动点,∠PAQ=∠BAO属于不变特征,
若两个直角三角形相似,只需要满足∠APQ或∠AQP等于90°.
③借助于相似三角形出现的比例关系建等式求解.
2.解题过程
由题意得,OA=3,OB=4,AB=5,AP=t,BQ=2t,AQ=5-2t.
①当∠APQ=90°时,如图所示,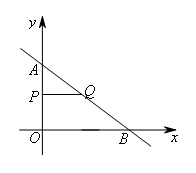
△APQ∽△AOB,
∴![]() ,
,
即![]() ,解得
,解得![]() .
.
②当∠AQP=90°时,如图所示,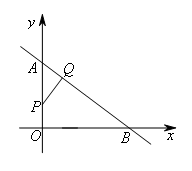
△APQ∽△ABO,
∴![]() ,
,
即![]() ,解得
,解得![]() .
.
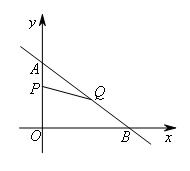
综上,符合题意的t的值为![]() .
.
略








