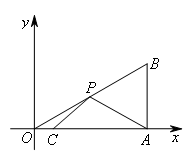
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为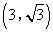 ,点C的坐标为
,点C的坐标为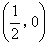 ,点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,点P为斜边OB上的一个动点,则PA+PC的最小值为( )
- A.
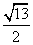
- B.
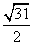
- C.

- D.
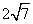
答案
正确答案:B
知识点:轴对称最值问题
如图,作点A关于OB的对称点D,连接CD交OB于P,此时PA+PC的值最小,即为CD.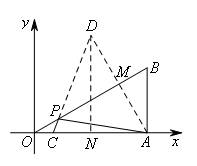
连接AD,过D作DN⊥OA于N,
∵![]() ,
,
∴![]() ,OA=3,
,OA=3,
∴∠AOB=30°,
∴![]() ,
,
∴AD=3,
在Rt△AND中,∠AND=90°,∠DAN=60°,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴在Rt△DNC中,由勾股定理得:![]() .
.
故选B.
略








