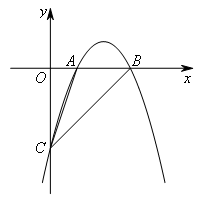
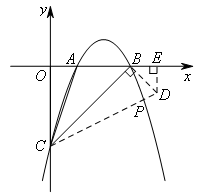
如图,二次函数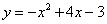 的图象交x轴于A,B两点(点A在点B的左侧),交y轴于点C.若在直线BC下方的二次函数图象上存在点P,使得∠PCB+∠ACB=45°,则点P的坐标为( )
的图象交x轴于A,B两点(点A在点B的左侧),交y轴于点C.若在直线BC下方的二次函数图象上存在点P,使得∠PCB+∠ACB=45°,则点P的坐标为( )
- A.(2,1)
- B.
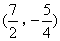
- C.(4,-1)
- D.
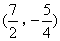 或(2,1)
或(2,1)
答案
正确答案:B
知识点:三等角模型 二次函数背景下的存在性问题
由题意易得∠OCB=∠OCA+∠ACB=45°,
要使得∠PCB+∠ACB=45°,只需∠OCA=∠PCB即可.
此时∠OCA固定,且![]() .
.
如图,过点B作CB的垂线,交直线CP于点D,过点D作DE⊥x轴于点E.
由题意得![]() ,
,
在Rt△BCD中,由![]() 得,
得,![]() .
.
易得∠EBD=45°,△EBD为等腰直角三角形,
∴BE=DE=1,
∴点D的坐标为(4,-1).
由C,D两点坐标可求得直线CD的表达式为![]() .
.
由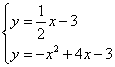 得,
得,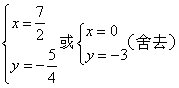 .
.
综上得,点P的坐标为![]() .
.
略








