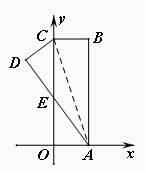
如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( )
- A.
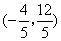
- B.
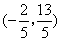
- C.

- D.
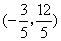
答案
正确答案:A
知识点:勾股定理 翻折变换(折叠问题)
过点D作DF⊥x轴,垂足为F,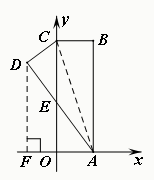
则△ADF∽△AEO,
又因为∠BAC=∠DAC,∠BAC=∠ACO,
所以∠DAC=∠ACO,
所以△AEC为等腰三角形.
设OE=x,则CE=EA=3-x,OA=1,
在Rt△AOE中,利用勾股定理,可得![]() ,
,
进而可得△AEO是一个三边比为3:4:5的直角三角形.则△ADF也是3:4:5的一个三角形,
而AD=3,进而可以求出点D的坐标为![]()
不清楚折叠的本质,找不到等量关系建立等式;








