如图,∠C=90°,点A,B分别在∠C的两边上,AC=30,BC=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B,C两点不重合时,作PD丄BC交AB于点D,作DE丄AC于点E,F为射线CB上一点,且∠CEF=∠ABC.设点P运动的时间为x秒(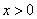 ).
).
(1)当点F落在CP上时,FP的长可以用含x的代数式表示为( )
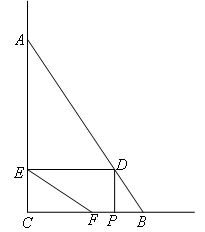
- A.
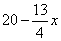
- B.
- C.
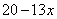
- D.
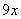
答案
正确答案:C
如图,当点F落在CP上时,要求FP的长,
已经知道了CB和BP的长,只需要表达出CF的长即可.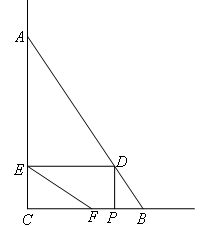
由题意得,Rt△DPB∽Rt△ACB,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵四边形ECPD为矩形,
∴EC=DP=6x.
在Rt△ECF和Rt△BCA中,
∵∠CEF=∠ABC,
∴Rt△ECF∽Rt△BCA,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
注意:运动速度为每秒4个单位长度,
∴BP的长为![]() .
.
A选项没有注意到运动速度;
B选项在计算结果时,没有减去BP的长(或者错误以为CP=20,把线段搞错);
D选项在于求出的是CF的长,忽略了最后结果是求FP的长.
略








