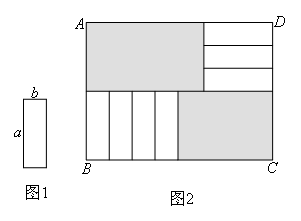
7张如图1所示的长为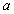 ,宽为
,宽为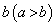 的小长方形纸片,按图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则
的小长方形纸片,按图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则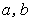 满足( )
满足( )
- A.
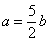
- B.
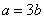
- C.
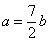
- D.
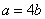
答案
正确答案:B
知识点:整式乘除的几何表示
解:如图所示,
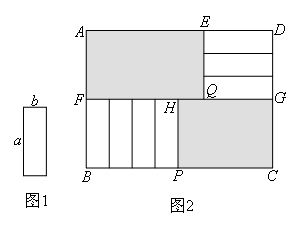
左上角阴影部分(即长方形AFQE)的长为AE,宽为AF=3b,
右下角阴影部分(即长方形PCGH)的长为PC,宽为a,
∵AD=BC,
即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE-PC=4b-a,
∴阴影部分面积之差为
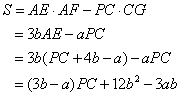
∵S始终保持不变,
∴S的值与PC的变化没有关系,
∴3b-a=0,即a=3b.
∴选B.
略








