如图，在Rt△ABC中，∠C=90°，∠A=60°，AC=4cm．长为1cm的线段MN在△ABC的边AB上沿AB方向以1（cm/s）的速度向点B运动（运动开始时点M与点A重合，结束时点N与点B重合），过点M，N分别作AB的垂线，交△ABC的直角边于P，Q两点，设线段MN运动的时间为t（s），四边形MNQP的面积为．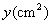

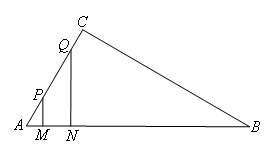
（1）线段MN运动的过程中，四边形MNQP为矩形时t的值为(    )，此时矩形的面积为(    )．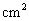

• A.
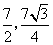
• B.
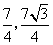
• C.
• D.

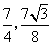
答案

正确答案：B

知识点：矩形的判定与性质  含30°角的直角三角形  图形运动产生的面积问题  

在Rt△ABC中，∠C=90°，∠A=60°，AC=4cm，
∴．
如图，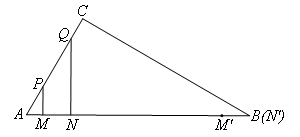

根据题意可知，点M运动的起点为点A，终点为点，其中，
∴点M运动的总路程为7cm．
由点M运动的速度为1（cm/s）可得M运动的总时间为7s，
∴线段MN的运动时间t的取值范围是（在0s和7s时四边形MNQP不存在）．
当四边形MNQP为矩形时，如图所示，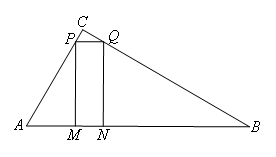

根据题意得，AM=t，AN=t+1，BN=7-t．
易求得，
要使得四边形MNQP为矩形，需PM=QN，即，
∴．
此时MN=1，，．

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>