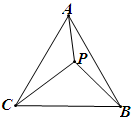
如图，P是等边三角形ABC内一点，AP=3，BP=4，CP=5，求∠APB的度数.

把△APC绕点C顺时针旋转60°到△B P₁C，连接PP₁，
则BP₁=AP=3，CP₁=CP=5，∠BP₁C=∠APC，∠2=∠1,
∵ ∠ACB=60°，∴ ∠PCP₁=60°。
∴ △PCP₁为等边三角形，PP₁=PC=5.
因为 在直角三角形PBP₁中，PB=4，BP₁=3，PP₁=5，所以∠PBP₁=90°，
在四边形CPBP₁中，∠CPB+∠CP₁B=360°-60°-90°=210°
∴ ∠APC+∠CPB=210°∴ ∠APB=360°-210°=150°

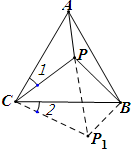
通过旋转，根据旋转前后的图形是全等的，从而实现边和角的转移，进而把分散的条件集中起来，利用勾股定理求解。