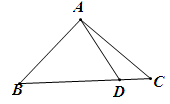如图所示，Rt△ABC中，∠BAC=90°，AB=AC，D为BC上任意一点．那么AD，BD，CD满足（   ）

过点A做∠BAE=∠CAD，并使AE=AD，连接BE，ED。
在△BAE和△CAD中，BA=CA，∠BAE=∠CAD，AE=AD，所以△BAE≌△CAD（SAS）
∴ CD=BE，∠C=∠ABE=45°，AD=AE
∵ ∠BAC=90°，∴ ∠EAD=90°，∠EBD=∠ABE+∠ABC=∠C+∠ABC=90°
在直角三角形AED中，ED²=AE²+AD²=2AD²
在直角三角形EBD中，ED²=BE²+BD²=CD²+BD²
∴ 2AD²=CD²+BD²

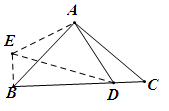
不能根据题目特征，利用旋转，把题目中一些分散的条件集中起来，进而构造直角三角形，利用勾股定理。