如图,钝角三角形ABC的面积为15,最长边AB=10,BD平分∠ABC,点M,N分别是BD,BC上的动点,则CM+MN的最小值为( )
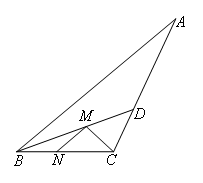
- A.3
- B.4
- C.5
- D.6
答案
正确答案:A
知识点:轴对称—最短路线问题 轴对称—最值问题
如图,过点N作BD的对称点E,连接CE,ME.
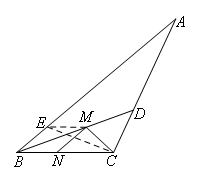
∵BD平分∠ABC,
∴点E落在AB上.
此时△MEB≌△MNB
∴ME=MN,
∴CM+MN=CM+ME,
∵![]() ,当C,M,E共线时,等号成立
,当C,M,E共线时,等号成立
∴CM+ME最小值为CE,
点C是AB外一点,E是AB上任意一点,则当CE⊥AB时,CE取最小值
此时根据面积公式可求![]() ,
,
即CE的最小值为3,
∴CM+MN的最小值为3.
略








