已知正方形ABCD中,O是对角线AC的中点,P是对角线AC上一动点,连接PB.
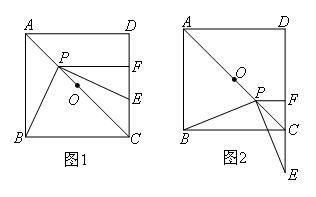
(1)过点P作PF⊥CD于点F,作PE⊥PB,且PE交CD(或CD的延长线)于点E,如图1和图2所示,则DF和FE的数量关系是( )
- A.
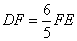
- B.
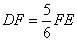
- C.DF=FE
- D.

答案
正确答案:C
知识点:正方形的性质 三角形全等的判定及性质 类比探究问题
分析:由于∠BPE为斜放置的直角,所以可以通过延长FP交AB于点G(横平竖直的线),补成弦图的方式,来处理问题.又因为在图1和图2中,PB⊥PE没有发生变化,PF⊥BC也没有发生变化,所以可采取相同的方式来分析,以图1为例(分析图2时直接照搬相同的字母,相同的辅助线,相同的思路即可).
如图,延长FP交AB于点G.
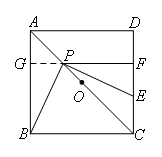
易知四边形AGFD是矩形,△AGP是等腰直角三角形,
∴AG=DF=GP,AD=GF=AB,
∴BG=PF.
又∵∠EFP=∠PGB,∠EPF=90°-∠GPB=∠PBG,
∴△EFP≌△PGB,
∴FE=GP,
∴DF=FE.
略








