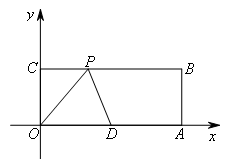
如图，在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A，C的坐标分别为A（10，0），C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为(    )

①如图，当OD为等腰三角形的腰时，分别以点O，点D为圆心，以OD长为半径画圆，
与线段BC有三个交点P₁，P₂，P₃，此时等腰△ODP的腰长都为5，都符合题意．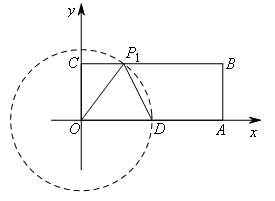

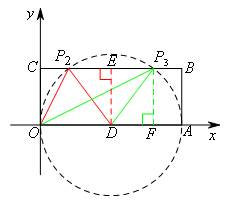
在Rt△OCP₁中，由勾股定理，得，
∴P₁（3，4）．
过点D作DE⊥BC于点E，
在Rt△DEP₂中，由勾股定理，得，
∴CP₂=2，
∴P₂（2，4）．
过点P₃作P₃F⊥OA于点F，
在Rt△P₃DF中，由勾股定理，得，
∴OF=8，
∴P₃（8，4）．
②如图，当OD为等腰三角形的底时，作线段OD的垂直平分线，交BC于点P₄，此时等腰三角形ODP的腰长为，不符合题意．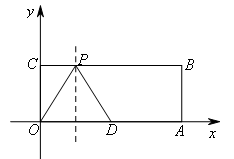

综上，答案选B．

略