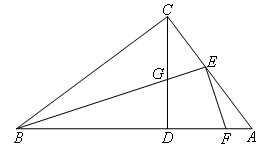
在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交
AB于点F,如图所示,若AC=mBC,CE=nEA(m,n为任意实数),则EF与EG的数量关系是( )
- A.
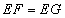
- B.
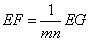
- C.

- D.
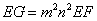
答案
正确答案:B
第3题和第2题的区别在于少了一个等腰直角三角形(线段相等),多出一个线段之间的关系(线段成比例),那么同样照搬第2题的辅助线和思路,在最后处理的时候,用线段间比例关系进行分析.
如图,过点E作EM⊥AB于点M,EN⊥CD于点N,
∵△AEM∽△ACD,
∴![]() ,即
,即![]()
∵△CEN∽△CAD,
∴![]() ,即
,即![]()
∵△EFM∽△EGN,
∴![]()
∵△CDA∽△BCA,
∴![]()
即AD=mCD,
∴![]()
∴![]() ,即
,即![]()
略








