已知CD是经过∠BCA的顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB,且∠BEC=∠CFA=∠α.
(1)如图,若∠BCA=90°,∠α=90°,则EF,BE,AF这三条线段之间的数量关系为(    )

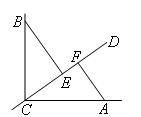
• A.BE=AF+EF
• B.BE=2EF
• C.BE=AF-EF
• D.BE=AF+2EF

答案

正确答案：A

知识点：全等三角形的判定  类比探究问题  

EF，BE，AF这三条线段之间的数量关系为BE=AF+EF．
证明如下：
∵∠BCA=90°，∠BEC=∠CFA=∠α=90°，
∴∠BCE+∠ACF=90°，∠ACF+∠CAF=90°，
∴∠BCE=∠CAF．
又∵CA=CB，
∴△BCE≌△CAF，
∴BE=CF，CE=AF．
∵CF=CE+EF，
∴BE=AF+EF．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>