如图,在△ABD中,C是BD的中点,∠BAC=90°,∠CAD=45°.若AC=2,则AB的长为(    )

1．思路点拨
看到中点，想到以下几种方法：与直角三角形结合利用直角三角形斜边中线等于斜边一半；与等腰三角形结合利用“三线合一”；另外就是倍长中线或者类倍长中线，结合题目中的条件，发现可以利用倍长中线法．

2．解题过程
如图，延长AC至点E，使得CE=AC，连接DE．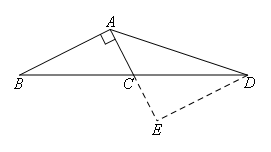

∵C是BD的中点，
∴BC=DC，
又∵∠ACB=∠ECD，
∴△ACB≌△ECD（SAS）
∴∠E=∠BAC=90°，DE=AB，
∵∠CAD=45°，
∴∠ADE=45°，
∴AE=DE，
∵AE=2AC，
∴AB=2AC，
∵AC=2，
∴AB=4．
3．易错点
对中点这个条件不敏感，所以需要同学们对于中点的几种用法进行总结，并能够结合题干条件选择合适的方法解决问题．

略