如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处.若BE=BO,则∠ABC的度数为( )(提示:三角形三条边的垂直平分线交于一点)
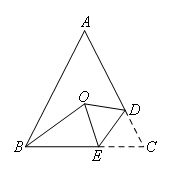
- A.54°
- B.60°
- C.63°
- D.72°
答案
正确答案:C
知识点:等腰三角形的性质 折叠问题 三角形三条边的垂直平分线交于一点
如图,连接OC,连接AO并延长.
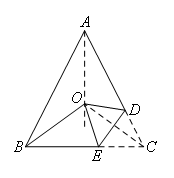
∵点O是三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠BOC=2∠BAC.
设∠OBC=x°,则∠OCB=x°,
由折叠的性质可知,OE=CE,
∴∠COE=∠OCB=x°,
∴∠OEB=2x°,
∵BE=BO,
∴∠BOE=∠OEB=2x°,
∴x+2x+2x=180,
解得:x=36,
∴∠BOC=3x°=108°,
∴![]() ,
,
∴![]() .
.
故选C.
略








