如图,将等腰△ABC沿DE折叠,使顶角顶点A落在两底角平分线的交点F处,若BF=DF,则∠C的大小是( )
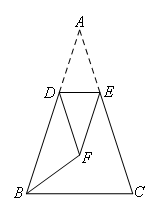
- A.80°
- B.75°
- C.72°
- D.60°
答案
正确答案:C
知识点:等腰三角形的性质 折叠问题 三角形三个内角的角平分线交于一点
如图,连接AF.
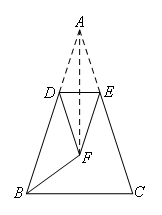
∵点F是三角形两底角平分线的交点,
∴点F是△ABC三个内角角平分线的交点,
∴∠DAF=∠EAF,
由折叠性质知,AD=DF,
∴∠DAF=∠DFA,
设∠DAF=x°,则∠DFA=x°,∠EAF=x°,
∴∠BDF=2x°,
∵BF=DF,
∴∠FBD=2x°,
∴∠ABC=4x°,
∵AB=AC,
∴∠C=∠ABC=4x°,
∴2x+4x+4x=180,
∴x=18,
∴∠C=4x°=72°.
故选C.
略








