 如图,直线
如图,直线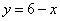 交x轴、y轴于A、B两点,P是反比例函数
交x轴、y轴于A、B两点,P是反比例函数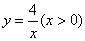 图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F.则
图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F.则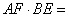
- A.8
- B.6
- C.4
- D.
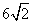
答案
正确答案:A
过点E作EC⊥OB于C,过点F作FD⊥OA于D,
∵直线y=6-x交x轴、y轴于A、B两点,
∴A(6,0),B(0,6),
∴OA=OB,
∴∠ABO=∠BAO=45°,
∴BC=CE,AD=DF,
∵PM⊥OA,PN⊥OB,
∴四边形CEPN与MDFP是矩形,
∴CE=PN,DF=PM,
∵P是反比例函数图象上的一点,
∴PN•PM=4,
∴CE•DF=4,
在Rt△BCE中,BE=![]() CE,
CE,
在Rt△ADE中,AF=![]() DF,
DF,
∴AF•BE=![]() DF•
DF•![]() CE=2DF•CE=8.
CE=2DF•CE=8.
不会把所求问题AF•BE与横平竖直的线段之积建立起联系







 如图,直线
如图,直线