已知:如图,在△ABC中,AB=AC=18,BC=12,点D为AB的中点.点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时点Q在线段CA上由C点向A点以每秒a个单位的速度匀速运动.设运动时间为t秒,若某一时刻△BPD与△CQP全等,则t的值与相应的点Q的运动速度a为(    )

1．思路分析
首先判断这是一道动点问题，对于动点问题，我们的解决套路是：
①研究基本图形，动点的运动状态；
②分析状态转折点，分段；
③表达线段长，建等式．
2．解题过程
（1）研究基本图形，动点的运动状态
基本图形是一个等腰三角形，且AB=AC=18，BC=12，点D为AB的中点，分析点P的运动时间可得0≤t≤4
（2）分析状态转折点，分段
此题中不涉及状态转折，所以跳过此步
（3）表达线段长，建等式
由题意知△BPD与△CQP全等，并未用全等符号连接，可知应该分类讨论，在△BPD与△CQP中，∠B=∠C，
∴B和C一定是对应顶点，可分成两种情况．
①当△BPD≌△CQP时，如图，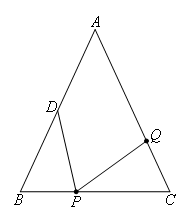


BP=CQ，BD=CP
在△ABC中，AB=AC=18，BC=12，
∵D为AB的中点，
∴BD=CP=9，
∴CQ=BP=3
又∵BP=3t，CP=12-3t
可得t=1
CQ=at
∴a=3
②当△BPD≌△CPQ时，如图，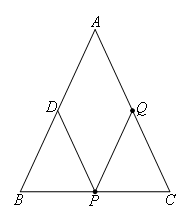

可知BP=CP=6
BD=CQ=9
∵BP=3t
∴t=2
而CQ=at
∴
综上：t=1，a=3或t=2，
故选C

略