如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=2,FD=4,则BC的长为( )

- A.
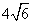
- B.
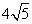
- C.
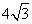
- D.
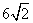
答案
正确答案:A
如图,连接EF.
∵CF=2,DF=4,
∴AB=CD=6.
∵点E是AD中点,
∴AE=ED.
由折叠可知,BG=BA=6,EG=AE,∠A=∠EGB=90°,
∴EG=ED.
在Rt△EGF和Rt△EDF中,
EG=ED,EF=EF,
∴△EGF≌△EDF(HL),
∴GF=DF=4,
∴BF=BG+GF=10.
在Rt△BCF中,由勾股定理得:![]()
∴![]()
故选A.
略








