已知:如图,在正方形ABCD,正方形CEFG中,BC=CD,CE=CG,∠BCD=∠ECG=90°,且B,C,F三点共线,连接BE交CD于M,连接DG分别交BE,CE,CF于N,P,Q.有以下结论:①BE=DG;②BM=DQ;③CM=CQ;
④∠BNQ=90°.其中正确结论的个数是( )
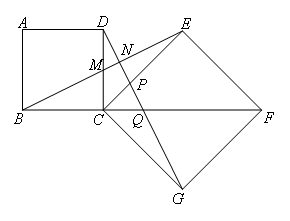
- A.1个
- B.2个
- C.3个
- D.4个
答案
正确答案:D
知识点:全等三角形的判定与性质
∵∠BCD=∠ECG=90°
∴∠BCD+∠DCE=∠ECG+∠DCE
即∠BCE=∠DCG
在△BCE和△DCG中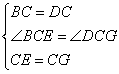
∴△BCE≌△DCG(SAS)
∴BE=DG,∠CBE=∠CDG
在△BCM和△DCQ中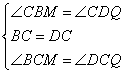
∴△BCM≌△DCQ(ASA)
∴BM=DQ,CM=CQ
∵∠CDG+∠CQD=90°,∠CBE=∠CDG
∴∠CBE+∠CQD=90°
∴∠BNQ=90°
综上,正确的选项为①②③④,共4个,故选D
略








