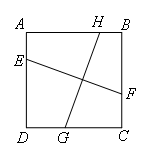
如图,正方形ABCD内有两条相交线段EF,GH,E,F,G,H分别在边AD,CB,DC,BA上,小颖认为若EF⊥GH,则EF=GH;小明认为:若EF=GH,则EF⊥GH.你认为(    )

（1）判断小颖说法是否正确，即若EF⊥GH，是否能推出EF=GH.
如图，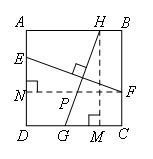

作HM⊥DC于点M，FN⊥AD于点N，FN交HG于点P
∵∠GHM+∠HPF=∠EFN+∠HPF=90°，
∴∠GHM=∠EFN，
∵∠HMG=∠ENF=90°，
HM=NF=AB，
在△FEN和△HGM中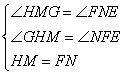

∴△FEN≌△HGM（ASA），
∴EF=GH，小颖说法正确．
（2）判断小明说法是否正确，即若EF=GH，是否能推出EF⊥GH.
①如图1，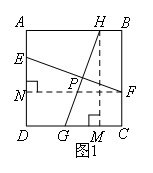

作HM⊥DC于点M，FN⊥AD于点N，FN交HG于点P
在Rt△FEN和Rt△HGM中

∴△FEN≌△HGM（HL），
∴∠EFN=∠GHM，
∴∠GHM+∠HPF=∠EFN+∠HPF=90°，
∴EF⊥GH，这时小明的说法正确；
②如图2，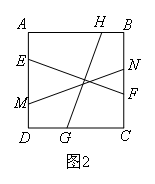

在AD上任取一点M，以EF的长为半径作圆，与正方形的BC边交于点N，则MN=EF=GH，但是此时不能保证MN⊥GH，小明的说法不对．
综上，小颖正确，小明不正确，选C

略