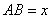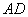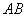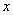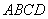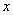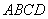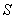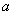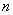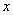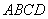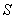（2011贵州）用长度一定的不锈钢材料设计成外观为矩形的框架（如图①②③中的一种）.设竖档米，请根据以上图案回答下列问题：（题中的不锈钢材料总长均指各图中所有黑线的长度和，所有横档和竖档分别与、平行）（1）在图①中，如果不锈钢材料总长度为12米，当为多少时，矩形框架的面积为3平方米？（2）在图②中，如果不锈钢材料总长度为12米，当为多少时，矩形框架的面积最大？最大面积是多少？（3）在图③中，如果不锈钢材料总长度为米，共有条竖档，那么当为多少时，矩形框架的面积最大？最大面积是多少？

答案

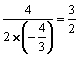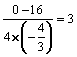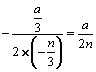解：（1）AD=（12-3x）÷3=4-x，列方程：x（4-x）=3，-4x+3=0，∴=1，=3，答：当x=1或3米时，矩形框架ABCD的面积为3平方米；（2）AD=（12-4x）÷3=4-x，S=x（4-x），=-+4x，当x=-时，=，答：当x=时，矩形架ABCD的面积S最大，最大面积是3平方米；（3）AD=（a-nx）÷3=-x，S=x（-x），=，当x=-时S最大=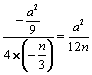．答：当x=时，矩形ABCD的面积S最大，最大面积是平方米．

知识点：二次函数的应用  

（1）先用含x的代数式（12-3x）÷3=4-x表示横档AD的长，然后根据矩形的面积公式列方程，求出x的值．（2）用含x的代数式（12-4x）÷3=4-x表示横档AD的长，然后根据矩形面积公式得到二次函数，利用二次函数的性质，求出矩形的最大面积以及对应的x的值．（3）用含x的代数式（a-nx）÷3=表示横档AD的长，然后根据矩形的面积公式得到二次函数，利用二次函数的性质，求出矩形的最大面积以及对应的x的值．

本题考查学生利用二次函数解决面积问题的能力．对于题意的理解不到位，不会表示长和宽，二次函数的最值不会求。本题考查的是二次函数的应用，（1）根据面积公式列方程，求出x的值．（2）根据面积公式得二次函数，利用二次函数的性质求最值．（3）根据面积公式得到字母系数的二次函数，然后求出函数的最大值．

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>