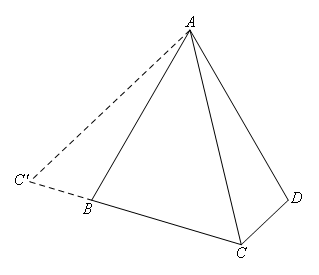
如图,凸四边形ABCD满足条件:AB=AD,∠BAD=60°,∠BCD=120°,则AC与BC+CD的数量关系为( )
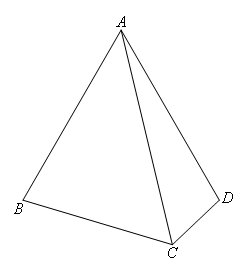
- A.
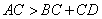
- B.
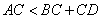
- C.
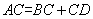
- D.不确定
答案
正确答案:C
知识点:作图—旋转变换
1.思路分析
本题主要考查在特殊条件下如何使用旋转思想解决问题.解决此类问题需要清楚:
①旋转是全等变换,旋转前后对应边、对应角相等;
②满足旋转三要素的情形下(如有等边、等腰直角),可以考虑旋转思想.
本题中有AB=AD,∠BAD=60°,∠BCD=120°,可考虑将△ACD顺时针旋转,使得AD与AB重合,此时可证![]() 为等边三角形,进而可知AC=BC+CD.
为等边三角形,进而可知AC=BC+CD.
2.解题过程
如图,延长CB至点![]() ,使
,使![]() ,连接
,连接![]() ,则
,则![]() .
.
∵∠BAD=60°,∠BCD=120°,
∴∠ABC+∠D=180°,
又∵∠ABC+![]() =180°,
=180°,
∴∠D=![]() .
.
在![]() 和△ADC中,
和△ADC中,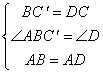
∴![]() ≌△ADC,
≌△ADC,
∴![]() ,
,![]() .
.
∵∠BAD=60°,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴AC=BC+CD.
故选C.
3.易错点
看到AB=AD的条件,没有使用旋转解决问题的意识,对旋转思想使用的前提条件不清楚.
错误使用三角形两边之和大于第三边,猜测结论.
略








