如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为( )

- A.
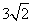
- B.
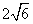
- C.
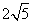
- D.
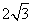
答案
正确答案:B
1.思路分析
本题主要考查折叠背景下勾股定理的使用,解决此类问题需要:
①读题标注,明确目标,梳理信息.
本题求线段BC的长,已知CF长,只需求出BF长,即可使用勾股定理计算BC的长.
②熟悉折叠性质,合理转化条件.
要清楚折叠是全等变换,折叠前后对应边、对应角相等.可据此得出BG=BA,结合点E是AD中点,可证得DF=GF,进而实现条件转移,结合勾股定理求解.
2.解题过程
如图,连接EF.
∵CF=1,DF=2,
∴AB=CD=3.
∵点E是AD中点,
∴AE=ED.
由折叠可知,BG=BA=3,EG=AE,∠A=∠EGB=90°,
∴EG=ED.
在Rt△EGF和Rt△EDF中,
EG=ED,EF=EF,
∴△EGF≌△EDF(HL),
∴GF=DF=2,
∴BF=BG+GF=5.
在Rt△BCF中,由勾股定理得:
BC2=BF2-CF2
∴![]() .
.
故选B.
3.易错点
没有通过中点及折叠的性质,找出DF=FG这一条件,导致条件不够,无法计算.
略








