已知:如图,在△ABC中,AB=AC,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是( )
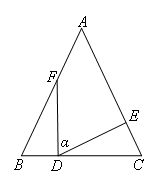
- A.2α+∠A=180°
- B.α+∠A=90°
- C.2α+∠A=90°
- D.α+∠A=180°
答案
正确答案:A
1.思路点拨:
由AB=AC,根据等边对等角,可知∠B=∠C,又由BF=CD,BD=CE,可证得
△BDF≌△CED(SAS),进而根据全等三角形的性质,可得∠B=∠C=α,
根据三角形的内角和定理,即可求得答案.
2.解题过程:
解:
∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中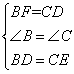
∴△BDF≌△CED(SAS),
∴∠BFD=∠EDC,
∵α+∠BDF+∠EDC=180°,
∴α+∠BDF+∠BFD=180°,
∵∠B+∠BDF+∠BFD=180°,
∴∠B=α,
∴∠C=∠B=α,
∵∠A+∠B+∠C=180°,
即2α+∠A=180°.
故选A.
3.易错点:
等腰三角形等边对等角的性质掌握不熟练;利用三角形内角和定理进行导角这种方法的使用不熟练.
略








