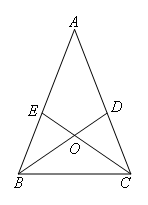
如图,在△ABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,
CE交AB于点E.某同学分析图形后得出以下结论:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;
④△BOE≌△COD;⑤△ACE≌△BCE;上述结论一定正确的是(    )

根据全等三角形的5种判定方法把5个结论逐一进行验证，也可以运用排除法．
先来分析一下题目，由AB=AC得到的是∠ABC=∠ACB，
再结合角平分线，可得∠ABD=∠CBD=∠ACE=∠BCE．
结论①：
在△BCD和△CBE中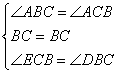

∴BCD≌△CBE（ASA）
故①正确；
结论②：
∠ABD=∠CBD，BD=BD，仅有两个条件，无法证明全等，故②错误；
结论③：
在△BDA和△CEA中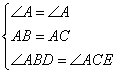

∴△BDA≌△CEA（ASA）
故③正确；
结论④：
由①可知BE=CD
在△BOE和△COD中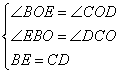

∴△BOE≌△COD（AAS）
故④正确；
结论⑤，道理和②一样，错误．
故正确结论为①③④，选D．

略