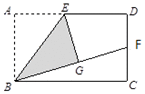
2010河南（1）操作发现如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．（2）问题解决保持（1）中的条件不变，若DC=2DF，求的值；（3）类比探求保持（1）中条件不变，若DC=nDF，求的值．

答案

⑴同意，连接EF，则∠EGF＝∠D＝90°，EG＝AE＝ED，EF＝EF．∴Rt△EGF≌Rt△EDF．∴GF＝DF．⑵由⑴知，GF＝DF．设DF＝x，BC＝y，则有GF＝x，AD＝y.∵DC＝2DF，∴CF＝x，DC＝AB＝BG＝2x．∴BF＝BG＋GF＝3x．在Rt△BCF中，BC²＋CF²＝BF²，即y²＋x²＝(3x)²．∴y＝2x，∴．⑶由⑴知，GF=DF，设DF＝x，BC＝y，则有GF＝x，AD＝y．∵DC＝n·DF，∴DC＝AB＝BG＝nx．∴CF＝(n－1)x，BF＝BG＋GF＝(n＋1)x．在Rt△BCF中，BC²＋CF²＝BF²，即y²＋[(n－1)x]²＝[(n＋1)x]²．∴y＝2x．∴（或）

知识点：勾股定理  规律探索型问题  

（1）结合折叠思路（找折痕、线段和角的转移）先研究特殊情况(2)由特殊情况推广到一般情况；（抓住折叠中的条件转移，找目标三角形）

（1）折叠实现条件的转移，由线段BG到BG长的转化，学生容易难以完成（2）学生不容易由“特殊”推广到“一般情况”

下载次数：4

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>