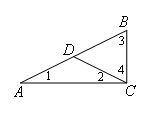
如图,下列说法:①若∠ACB=90°,AD=BD,则AD=BD=CD;②若∠ACB=90°,AD=CD,
则AD=BD=CD;③若∠ACB=90°,BD=CD,则AD=BD=CD.其中正确的个数是( )
- A.0
- B.1
- C.2
- D.3
答案
正确答案：D
知识点：直角三角形两锐角互余 直角三角形斜边中线等于斜边一半
①如图，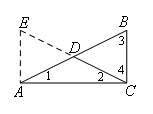
延长CD到E，使得DE＝CD，连接AE，
在△BDC与△ADE中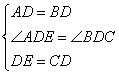
∴△ADE≌△BDC（SAS）
∴∠3＝∠DAE，AE＝BC
∵∠1+∠3＝90°
∴∠1+∠DAE＝90°，即：∠EAC＝90°
在△ABC与△CEA中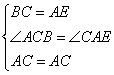
∴△ABC≌△CEA（SAS）
∴AB＝CE
∵AB＝2AD＝2BD，CE＝2CD
∴AD=BD=CD
故①正确；
②∵∠ACB=90°
∴∠1+∠3＝90°
∵AD=CD
∴∠1＝∠2
∴∠3＝∠4
∴BD=CD
综上：AD=BD=CD
故②正确
③证明方法同②，可得③正确
故选D
略
WORD格式（
