如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于(    )

第一步：分析条件，探索思路：∠1和∠2无法单独求解，故需作为一个整体求出它们的和
第二步：设计解决方案：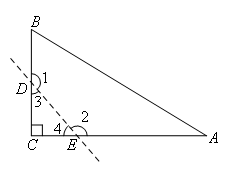

①可以看作是四边形ABDE的内角，则∠1+∠2=360°-∠A-∠B，根据题意，在Rt△ABC中，
∠A+∠B=90°。则可求出∠1+∠2=270°；
②将∠1，∠2看成是△CDE的两个外角，可知：∠1=∠4+∠C，∠2=∠3+∠C，
∴∠1+∠2=∠4+∠C+∠3+∠C
=（∠4+∠C+∠3）+∠C
=180°+90°
=270°
第三步：具体操作，选取第二种方法为例：
解：如图，

∵∠1，∠2是△CDE的外角，
∴∠1=∠4+∠C，∠2=∠3+∠C，
即∠1+∠2=∠4+∠C+∠3+∠C
=（∠4+∠C+∠3）+∠C
=180°+90°
=270°
故选B．

略