在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与
△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有( )
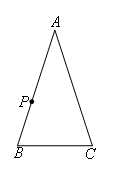
- A.1
- B.3
- C.4
- D.
5
答案
正确答案:B
知识点:相似三角形的判定与性质
如图所示:
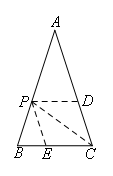
①过点P作PD∥BC交AC于点D,则△APD∽△ABC,
②过点P作PE∥AC交BC于点E,则△BPE∽△BAC,
③连接PC,
∵∠A=36°,AB=AC,点P在AC的垂直平分线上,
∴AP=PC,∠ABC=∠ACB=72°,
∴∠ACP=∠PAC=36°,
∴∠PCB=36°,
∴∠B=∠B,∠PCB=∠A,
∴△CPB∽△ACB
故过点P的△ABC的相似线最多有3条,即PC,PD,PE.
略








