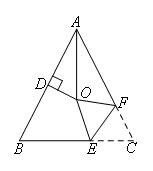
如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为(    )

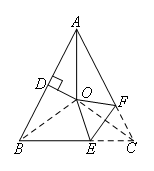
如图，连接OB，OC
∵∠BAC=54°，AO为∠BAC的平分线
∴∠BAO=∠BAC=×54°=27°
∵AB=AC
∴∠ABC=(180°-∠BAC)=(180°-54°)=63°
∵DO是AB的垂直平分线
∴OA=OB
∴∠ABO=∠BAO=27°
∴∠OBC=∠ABC-∠ABO=63°-27°=36°
∵AO为∠BAC的平分线，AB=AC
∴AO所在的直线是BC边的垂直平分线
∴OB=OC
∴∠OCB=∠OBC=36°
∵将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合
∴OE=CE
∴∠COE=∠OCB=36°
在△OCE中，∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°
故选C．

略