如图,把长方形ABCD对折,折痕为MN(图1),展开后再折叠,使点B落在折痕MN上的B′处,得到Rt△AB′E(图2),延长EB′交AD于点F,则∠EFA等于( )
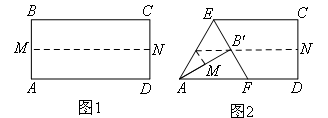
- A.45°
- B.60°
- C.75°
- D.无法确定
答案
正确答案:B
(1)考点:折叠的性质,垂直平分线的性质
(2)解题过程:
解: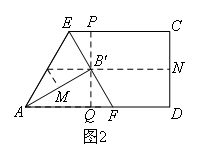
如图,过点B′作CD的平行线分别交EC,AD于点P,Q
∵EC∥FD,
∴∠PEB′=∠QFB′,∠PB′E=∠FB′Q
由折叠得:PB′=QB′
∴△PEB′≌△QFB′
∴EB′=B′F
∵AB′⊥EF
∴AE=AF
∴∠EFA=∠AEF
∵EC∥FD
∴∠FEC=∠EFA
∴∠FEC=∠AEF
∵∠FEC+2∠AEF=180°
∴3∠AEF=180°
∴∠AEF=60°
∴∠EFA=60°
故选B
略








