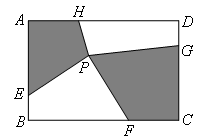
如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,P为矩形ABCD内一点.
若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,则四边形PFCG的面积为(    )

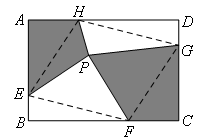
四边形PFCG是不规则四边形，结合图形，考虑将其分成两个三角形的面积进行求解；
如图，连接HE，GF，EF，GH，容易证明四边形HEFG是平行四边形（利用三角形全等可以证明两组对边分别相等）．

∵，，
∴，
∵点P是平行四边形HEFG内一点，
∴
（HE，GF相等，当作底，两个三角形的高之和与平行四边形的高相等）．
∵=5-3=2，
∴=7-2=5，
∴四边形PFCG的面积=

略