如图,E,F是正方形ABCD的边AD上的两个动点,且满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是( )

- A.1
- B.2
- C.
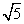
- D.
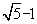
答案
正确答案:D
知识点:正方形的性质 中考数学几何中的最值问题
①求DH的最小值,我们发现正方形的顶点D是固定点,H是动点,
我们需要研究H的位置是否具有关键性质,这个时候需要进行边角关系的研究;
②由题干条件我们知道△EAB≌△FDC,则∠ABE=∠DCF,而△DGA≌DGC(SAS),
∴∠DAG=∠DCG,
∴∠DAG=∠ABE,
∵∠DAG+∠HAB=90°,
∴∠ABE+∠HAB=90°,
∴AH⊥HB,
这个时候我们得到了垂直关系,知道△HAB是直角三角形;
③结合最值问题中常用的三个定理,我们取AB中点M,连接HM,DM,如图所示: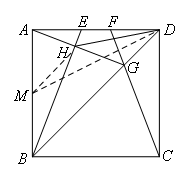
此时DH≥DM-HM,且这三点共线时,取等号,此时DH=DM-HM,
易求得HM=1,![]() ,
,
∴![]() ,至此得出DH的最小值为
,至此得出DH的最小值为![]() ,
,
故选D.
略








