如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=.在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的值最小,则此时AM+NB=(    )

如图，作点A关于直线a的对称点A′，连接A′B交直线b于点N，
过点N作NM⊥直线a于点M，连接AM．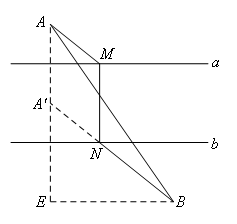

∵点A到直线a的距离为2，a与b之间的距离为4，
∴AA′=MN=4，
∴四边形AA′NM是平行四边形，
∴AM+NB=A′N+NB=A′B．
此时AM+MN+NB=A′B+NB，其值最小．
过点B作BE⊥AA′，交AA′的延长线于点E，
易得AE=2+4+3=9，，A′E=2+3=5，
在Rt△AEB中，，
在Rt△A′EB中，．
故选B．

略