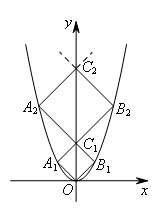
如图,已知点A1,A2,…,A2013在函数y=x2位于第二象限的图象上,点B1,B2,…,B2013在函数y=x2位于第一象限的图象上,点C1,C2,…,C2013在y轴的正半轴上,若四边形OA1C1B1,四边形C1A2C2B2,…,四边形C2012A2013C2013B2013都是正方形,则正方形C2012A2013C2013B2013的边长为( )
- A.2012
- B.2013
- C.
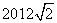
- D.
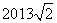
答案
正确答案:D
知识点:二次函数综合题
∵OA1C1B1是正方形,
∴直线OB1与y轴的夹角为45°,
∴直线OB1的解析式为y=x,联立![]() ,解得
,解得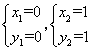 ,
,
∴B1(1,1),OB1=![]() ,
,
∵OA1C1B1是正方形,
∴OC1=![]() OB1=
OB1=![]() ×
×![]() =2,
=2,
∵C1A2C2B2是正方形,
∴C1B2的解析式为y=x+2,联立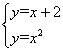 ,解得
,解得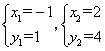 ,
,
∴B2(2,4),C1B2=![]() ,
,
∵C1A2C2B2是正方形,
∴C1C2=![]() C1B2=
C1B2=![]() =4,
=4,
∴C2B3的解析式为y=x+(4+2)=x+6,
联立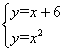 ,解得
,解得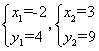 ,
,
∴点B2(3,9),C2B3=![]() ,…,
,…,
依此类推,正方形C2012A2013C2013B2013的边长C2012B2013=![]() .故选D.
.故选D.
略








