如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E，F分别是AC，BC的中点，直线EF与⊙O交于G，H两点．若⊙O的半径为14，则GE+FH的最大值为____．

如图，连接OA，OB．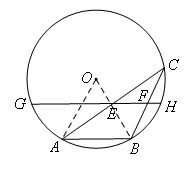

∵∠ACB=30°，
∴∠AOB=2∠ACB=60°，
∵OA=OB，
∴△AOB为等边三角形，
∴AB=OA=OB=14，
∵点E，F分别是AC、BC的中点，
∴EF=AB=7，
要求GE+FH的最大值，即求GE+FH+EF（弦GH）的最大值，
∵弦GH的最大值为直径的长度28，
∴GE+FH的最大值为21．

略