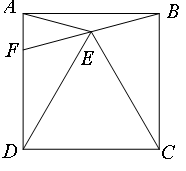
2. （2011贵州贵阳）如图，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB、EA，延长BE交边AD于点F.
（1）求证: △ADE≌△BCE；
（2）求∠AFB的度数.
答案
（1）证明：∵ABCD是正方形
∴AD=BC，∠ADC=∠BCD=90°
又∵△CDE是等边三角形
∴CE=CD，∠EDC=∠ECD=60°
∴∠ADE=∠ECB
∴△ADE≌△BCE．
（2）解：∵△CDE是等边三角形，
∴CE=CD=BC
∴△CBE为等腰三角形，且顶角∠ECB=90°-60°=30°
∴∠EBC= （180°-30°）=75°
∵AD∥BC
∴∠AFB=∠EBC=75°．
知识点：正方形的性质
全等找三组相等的条件即可，第二问是难点，怎样得出∠AFB的度数，我们要注意到平行后的内错角关系，还有△BCE为等腰三角形
无法找到∠AFB与其余角度的关系
WORD格式（
