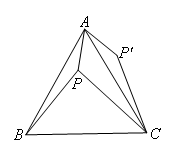
如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=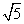 ,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´处,则sin∠PCP′的值是( )
,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´处,则sin∠PCP′的值是( )
- A.
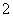
- B.

- C.
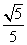
- D.
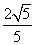
答案
正确答案:C
如图,连接PP′,
由旋转可知,∠PAP′=60°,AP′=AP=1,CP′=BP=2.
∴△APP′是等边三角形,PP′=1.
在△PCP′中,PC=![]() ,PP′=1,CP′=2.
,PP′=1,CP′=2.
∴PC2=P′P2+P′C2.
∴△PCP′是直角三角形,且∠PP′C=90°.
∴sin∠PCP′=![]() .故选C.
.故选C.
略








